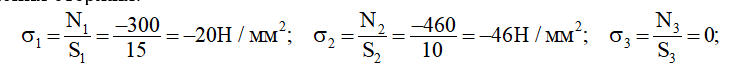Цель задания: определение внутренних усилий в сечениях элементов стержня переменной площади и длины; определение напряжений в поперечных сечениях стержня; определение абсолютных деформаций по длине стержня; построение соответствующих эпюр.
Дано:
| № | а, мм | S, мм2 | P1, H | Р2, Н | n1 | n2 | n3 | m1 | m2 | m3 |
| 20 | 48 | 10 | 460 | 160 | 1,5 | 1 | 1,5 | 1 | 1,5 | 1 |
Решение: В соответствии с заданными значениями n и m имеем:
- Определяем реакцию в заделке из условия равновесия:
Отсюда:
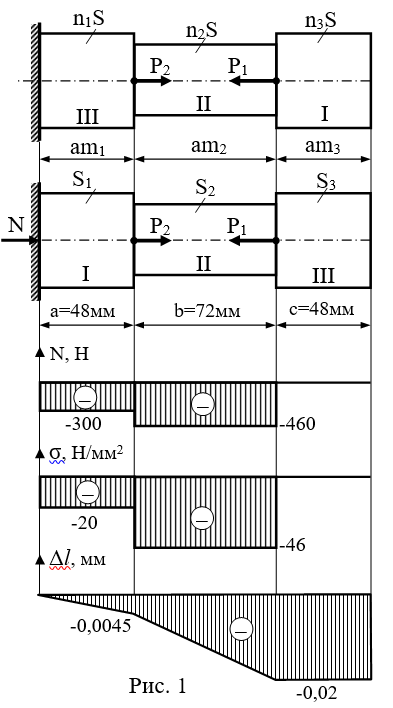
Разбиваем стержень на три участка I, II, III по точкам приложения сил и границам сечений.
В стержне действует только один силовой фактор – продольные силы, определяемые нагрузками Р1 и Р2.
- Методом сечений определяем продольные силы, предварительно полагая, что все участки стержня растянуты.
I участок: 0 ≤ х1 ≤ а = 48мм;
II участок: 0 ≤ х2 ≤ b = 72мм.
III участок: 0 ≤ х3 ≤ с = 48мм;
Т.о. участки I и II стержня сжаты, так как продольные силы получились отрицательными, а участок III не нагружен.
- Находим нормальные напряжения на каждом участке в зависимости от сечения стержня:
Эпюры продольных сил и нормальных напряжений построены на рисунке 1.
- Определяем изменение длины участков. Условием не задан модуль упругости первого рода. Принимаем его равным Е = 2,15∙105Н/мм2:
Т.о. брус сожмётся (укоротится) на 0,02 мм. Эпюра перемещений построена на рисунке 1.