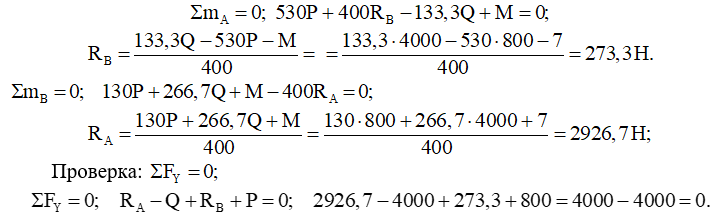Задача №3. Деформация изгиба.
Цель задания: Определение реакций в опорах в зависимости от различных внешних воздействий (распределённой нагрузки q, сосредоточенной силы Р и изгибающего момента М) и построение эпюры изгибающих моментов для расчёта схемы с двумя консолями, и момент сопротивления сечения WX для исходного вида сечения.
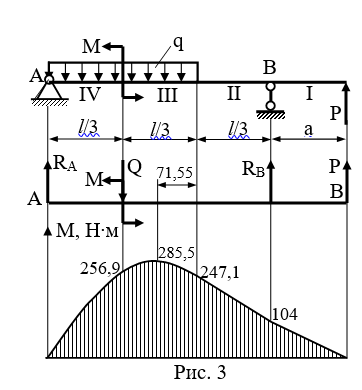
Решение: Схема балки в масштабе показана на рисунке 3.
- Для построения эпюры изгибающих моментов определим опорные реакции. Для этого отбросив связи, заменяем их действие искомыми реакциями. Т.к. внешних нагрузок в горизонтальном направлении нет, то реакции опор RА и RB направляем вертикально вверх.
Распределённую нагрузку заменим сосредоточенной нагрузкой, приложенной в центре участка:
Составляем уравнения равновесия:
- Составляем уравнения изгибающих моментов по участкам и строим их эпюру. Для этого делим балку на 4 участка I, II, III, IV по точкам приложения нагрузок и для каждого участка в произвольном сечении определяем изгибающие моменты.
На участках с распределённой нагрузкой изгибающий момент изменяется по параболе, выпуклой вверх. На этих участках эпюра может иметь экстремум в точке, где производная эпюры М3 или М4 обращается в ноль:
Эпюра изгибающих моментов показана на рисунке 3. Максимальное значение момента
На границе между участками III и IV эпюра моментов имеет скачок равный , но поскольку слева значение момента 256891Н∙мм, а справа , то скачок из-за его малости на рисунке эпюры не показан.
- Требуемый момент сопротивления сечения:
Квадратная балки по расходу металла экономичнее круглой балки, т.к. её сечение на 11% меньше, чем у круглой балки.